14.4. Задачі кінематики
Спеціальні системи координат. Віссю обертальної пари (i, i + 1), складеної з ланок i та (i + 1), є вісь циліндричного шарніра, жорстко зв’язана з ланкою i, навколо якої обертається ланка (i + 1). Для поступальної пари (і, і + 1) віссю є будь-яка пряма, паралельна вектору швидкості поступального руху ланки (і + 1) відносно ланки і.
Пронумеруємо усі ланки маніпулятора від стійки (ланка 0) до схвата (ланки n) і зв’яжемо з кожною з них свою систему декартових координат, вибрану наступним спеціальним чином: вісь zi проходить по осі кінематичної пари (і, і + 1); початок координат системи і, жорстко зв’язаної з ланкою і, лежить на спільному перпендикулярі до осей zi-1 і zi, або в точці їхнього перетину, якщо така є, або в будь-якій точці осі кінематичної пари, якщо вісь zi збігається з віссю zi-1 чи паралельна їй; вісь xi проходить по спільному перепендикуляру, проведеному до осей zi-1 і zi, і направлена від точки перетину цього перпендикуляра з віссю zi-1 до точки його перетину з віссю zi (чи в будь-який бік по нормалі до площини, що містить осі zi-1 і zi , якщо вони перетинаються, чи довільним чином, якщо zi-1 і zi проходять по одній прямій); вісь yi вибирається за правилом правої трійки векторів.
Початок координат системи 0, тобто системи, жорстко зв’язаної зі стійкою, може лежати в будь-якій точці осі пари (0, 1), вісь x0 направляється довільним чином.
Вибір системи n теж випадає зі спільного правила, оскільки ланка (n + 1) відсутня. Тому пропонується представити будь-якого типу пару (n, n + 1) і після цього вибрати систему за загальним правилом. Початок вибраної таким чином системи називається центром схвата.
1) поворот (i
– 1) системи навколо осі zi-1
на кут ![]() доти, доки вісь
xi-1 не стане паралельною
осі xi;
доти, доки вісь
xi-1 не стане паралельною
осі xi;
2) зсув поверненої системи вздовж осі zi-1 на величину si доти, доки осі xi-1 та xi не виявляться на одній прямій;
3) зсув вздовж осі xi на величину ai доти, доки не співпадуть початки координат;
4) поворот навколо
осі xi на кут ![]() до суміщення осі zi-1
з віссю zi.
до суміщення осі zi-1
з віссю zi.
Кожному з цих елементарних рухів відповідає одна з В-матриць [17]. Результуюча матриця переходу, що зв’язує системи (i – 1) та i, є добутком цих матриць:
Після перемноження одержуємо:
Відповідно до формули (П.34) з [17] за допомогою матриці Ai можна зв’язати радіуси-вектори однієї й тієї ж точки в системах і та (i - 1):
де
![]() – матриця-стовпець,
що визначає положення довільної точки ланки і у системі відліку, жорстко
зв’язаній з цією ланкою;
– матриця-стовпець,
що визначає положення довільної точки ланки і у системі відліку, жорстко
зв’язаній з цією ланкою;
![]() – матриця-стовпець,
що визначає положення тієї ж точки в системі, жорстко
зв’язаній з ланкою (i - 1).
– матриця-стовпець,
що визначає положення тієї ж точки в системі, жорстко
зв’язаній з ланкою (i - 1).
У матрицю Ai
входять чотири параметри: ![]() .
Для будь-якої кінематичної пари три з них повинні бути
константами і тільки один – змінною величиною. Для обертальної пари змінною
величиною є кут
.
Для будь-якої кінематичної пари три з них повинні бути
константами і тільки один – змінною величиною. Для обертальної пари змінною
величиною є кут ![]() , а для
поступальної пари – переміщення si.
Таким чином, кожна матриця Ai
містить тільки одну змінну величину, яку будемо надалі називати узагальненою
координатою і позначати qi.
, а для
поступальної пари – переміщення si.
Таким чином, кожна матриця Ai
містить тільки одну змінну величину, яку будемо надалі називати узагальненою
координатою і позначати qi.
Приклад складання таблиці кінематичних пар і параметрів і обчислення матриць Ai розглянутий у [17].
Задача розв’язується за допомогою формули:
де Tn – матриця, що дорівнює добутку матриць Ai:
У формулі (14.4) Rn
і R0 – матриці-стовпці розміром 4 ![]() 1, перші три елементи яких – це координати довільної точки схвата відповідно
в системах n і 0.
1, перші три елементи яких – це координати довільної точки схвата відповідно
в системах n і 0.
Стовпці матриці Tn
мають геометричне тлумачення. Перші три елементи першого, другого і третього
стовпців представляють собою напрямні косинуси відповідно осей ![]() у системі 0, а три елементи четвертого стовпця – це координати
у системі 0, а три елементи четвертого стовпця – це координати ![]() центра схвата в тій же системі:
центра схвата в тій же системі:
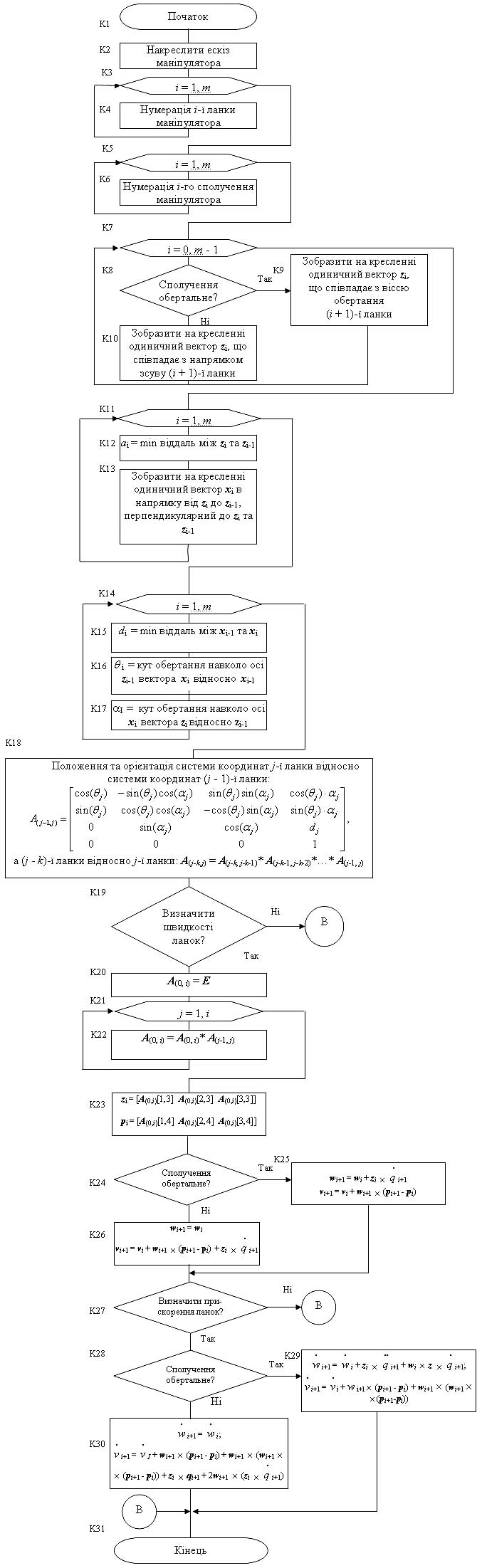
Отже, розв’язок прямої задачі кінематики маніпуляторів зводиться до того, що, задавшись значеннями узагальнених координат, обчислюються за допомогою (14.5) і (14.2) значення елементів матриці Tn, а отже, згідно з (14.6), визначаються положення та орієнтація схвата в системі координат, жорстко зв’язаній зі стійкою маніпулятора (відповідний алгоритм показаний на рис. 14.2).
Якщо потрібно визначити положення та орієнтацію не схвата, а деякої проміжної ланки і та радіус-вектор його точки в базовій (0) системі координат (схема відповідного алгоритму наведена на рис. 14.3), то необхідно скористатися формулами, аналогічними (14.4) і (14.5):
де
За такими ж формулами можна визначити положення та орієнтацію деякої ланки l відносно ланки і (відповідний алгоритм показаний на рис. 14.4):
де
Приклад розв’язання прямої задачі про положення розглянутий у [17].
Задати положення схвата, як і будь-якого твердого тіла, можна за допомогою шести величин. Звичайно три з них – це координати центра схвата, ще дві – це напрямні косинуси однієї з координатних осей схвата й остання – це один з напрямних косинусів іншої координатної осі схвата. Наприклад, цими шістьма величинами можуть бути шість наддіагональних елементів матриці Tn:
Прирівнюючи шість заданих величин до відповідних елементів матриці Tn, одержимо систему шести рівнянь (в загальному випадку трансцендентних), невідомими в яких є узагальнені координати.
Умовою існування розв’язку оберненої задачі є рівність n =
m, тобто можливість складання n рівнянь з n невідомими.
Але на відміну від прямої задачі, де стан ЗП однозначно визначається конфігурацією
МС, обернене відображення з шестивимірного робочого простору у простір узагальнених
координат у допустимій області зміни останніх, як правило, навіть при n
= 6 не є однозначним, тобто одному стану ЗП відповідає деяка множина
конфігурацій ![]() .
.
При n < m розв’язок оберненої задачі кінематики МС у загальному вигляді відсутній. Але й умова n = m не є достатньою для розв’язання цієї задачі, що пов’язано з типом і розподілом кінематичних пар. Тоді вдаються до штучного зменшення числа довільно заданих координат ЗП.
При n > m обернена задача кінематики МС розв’язується неоднозначно. У цьому випадку довільно задають (n -
m) узагальнених координат ![]() ,
а решту m цих координат знаходять, розв’язуючи задачу. При n > m кажуть, що МС має надлишкові
ступені рухомості, завдяки чому забезпечується можливість роботи МС у середовищі
з перешкодами чи за наявності у МС обмежень конфігурації.
,
а решту m цих координат знаходять, розв’язуючи задачу. При n > m кажуть, що МС має надлишкові
ступені рухомості, завдяки чому забезпечується можливість роботи МС у середовищі
з перешкодами чи за наявності у МС обмежень конфігурації.
Алгоритм розв’язання оберненої кінематичної задачі методом послідовних наближень. Не завжди обернену кінематичну задачу вдається розв’язати аналітично. При чисельному розв’язанні використовують комп’ютер, що вимагає програми чисельного розв’язку системи трансцендентних рівнянь. Тут наводиться найпростіший алгоритм чисельного розв’язання такої системи (схема відповідного алгоритму наведена на рис. 14.5).
Завдання полягає у відшуканні значень n узагальнених
координат по заданих n елементах матриці Tn,
причому ![]() . Для простоти
викладення будемо вважати, що маніпулятор має шість ступенів рухомості
і m = n = 6. Тоді шуканими є всі узагальнені
координати маніпулятора, які позначимо
. Для простоти
викладення будемо вважати, що маніпулятор має шість ступенів рухомості
і m = n = 6. Тоді шуканими є всі узагальнені
координати маніпулятора, які позначимо ![]() .
Заданими вважаємо шість наддіагональних елементів матриці Tn
(див. (14.11)). Значення qi
визначимо методом послідовних наближень.
.
Заданими вважаємо шість наддіагональних елементів матриці Tn
(див. (14.11)). Значення qi
визначимо методом послідовних наближень.
У нульовому наближенні дамо узагальненим координатам довільні початкові значення
![]() . Опишемо один крок одержання
уточнених значень узагальнених координат за відомими
наближеними значеннями.
. Опишемо один крок одержання
уточнених значень узагальнених координат за відомими
наближеними значеннями.
Нехай k – номер кроку. Наближене значення узагальненої координати qi
позначимо ![]() , а уточнене
–
, а уточнене
– ![]() (для першого кроку
наближене значення –
(для першого кроку
наближене значення – ![]() ,
уточнене –
,
уточнене – ![]() . Представимо
залежність матриці Tn
від узагальнених координат у вигляді
відрізка степеневого ряду Тейлора, обмеженого лінійними
членами, з центром розкладу в точці
. Представимо
залежність матриці Tn
від узагальнених координат у вигляді
відрізка степеневого ряду Тейлора, обмеженого лінійними
членами, з центром розкладу в точці ![]() :
:
де
![]() – матриця T6,
елементи якої виражені через наближені значення узагальнених координат.
– матриця T6,
елементи якої виражені через наближені значення узагальнених координат.
Введемо позначення:
причому
Uij,
– це матриця 4 ![]() 4:
4:
Із врахуванням (14.14) вираз (14.12) має вигляд:
Одній матричній рівності (14.15) відповідають 16 скалярних рівностей (по числу елементів матриці T6). Оскільки шість наддіагональних елементів матриці T6 задані, то відповідні їм рівності утворять систему лінійних рівнянь для шести узагальнених координат:
Оскільки наближені значення 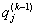 відомі, то система
(14.16) дозволяє визначити уточнені значення
відомі, то система
(14.16) дозволяє визначити уточнені значення ![]() .
На цьому закінчується k-й крок методу послідовних наближень. Далі, уточнені значення
.
На цьому закінчується k-й крок методу послідовних наближень. Далі, уточнені значення ![]() позначаються
позначаються ![]() і за їх
допомогою за формулами (14.5) і (14.13)
обчислюються матриці
і за їх
допомогою за формулами (14.5) і (14.13)
обчислюються матриці ![]() і
і ![]() . Процедура пошуку
. Процедура пошуку
![]() із системи (14.16)
повторюється.
із системи (14.16)
повторюється.
У випадку, коли маніпулятор має m < 6 ступенів рухомості і число невідомих узагальнених координат дорівнює m, система лінійних рівнянь, аналогічна (14.16), може бути записана таким чином:
де
![]() –
номер рядка, а
–
номер рядка, а ![]() – номер стовпця матриці Tn,
на перетині яких стоїть елемент, значення якого задане.
Очевидно, що кількість заданих елементів повинна дорівнювати n.
– номер стовпця матриці Tn,
на перетині яких стоїть елемент, значення якого задане.
Очевидно, що кількість заданих елементів повинна дорівнювати n.
У деяких задачах може знадобитися забезпечення заданого положення не схвата, а якої-небудь проміжної ланки i. У цьому випадку система (14.17) має вигляд:
Визначення законів зміни узагальнених координат при русі точки схвата по заданій траєкторії. Фактично приходиться вирішувати серію подібних задач для різних положень схвата.
Приймемо, що закон руху схвата відомий і потрібно знайти закони зміни узагальнених координат вздовж траєкторії центра схвата.
Нехай ![]() – тривалість майбутнього
переміщення схвата, tl
– момент закінчення інтервалу l. Розділимо
– тривалість майбутнього
переміщення схвата, tl
– момент закінчення інтервалу l. Розділимо ![]() на L малих інтервалів, наприклад, однакової довжини. На
початку інтервалу 1, тобто в момент t0,
відомі узагальнені координати, а наприкінці цього інтервалу, тобто в момент
t1, відоме положення схвата. Щоб
знайти узагальнені координати в момент t1,
потрібно розв’язати обернену задачу.
При цьому за початкове наближення можна взяти значення узагальнених координат
у момент t0. Це – хороше початкове
наближення і тим краще, чим менший інтервал часу (t0,
t1). Якщо число L вибране
досить великим, то початкове наближення виявиться таким хорошим, що досить буде
зробити один крок.
на L малих інтервалів, наприклад, однакової довжини. На
початку інтервалу 1, тобто в момент t0,
відомі узагальнені координати, а наприкінці цього інтервалу, тобто в момент
t1, відоме положення схвата. Щоб
знайти узагальнені координати в момент t1,
потрібно розв’язати обернену задачу.
При цьому за початкове наближення можна взяти значення узагальнених координат
у момент t0. Це – хороше початкове
наближення і тим краще, чим менший інтервал часу (t0,
t1). Якщо число L вибране
досить великим, то початкове наближення виявиться таким хорошим, що досить буде
зробити один крок.
Одержавши узагальнені координати для моменту t1,
можна використовувати їх як початкове наближення при розв’язку оберненої задачі для моменту t2
і т.д., поки не буде пройденого крок за кроком уся траєкторія аж до моменту
tL
– кінця загального інтервалу ![]() .
Ще краще за початкові значення для моментів tl,
починаючи з l = 2, брати величини:
.
Ще краще за початкові значення для моментів tl,
починаючи з l = 2, брати величини:
При заданій точності необхідного обчислення існує таке значення L, при якому обсяг обчислень мінімальний. При цьому необхідна точність досягається вже при першому наближенні. Зробивши L більшим, ми повинні будемо розв’язати більше обернених задач. Зробивши L меншим, ми одержимо менше обернених задач, але зате в кожній з них прийдеться обчислювати друге наближення (схему відповідного алгоритму наведено на рис. 14.6).
Приклади визначення законів зміни узагальнених координат маніпулятора розглянуті у [17, 19].
Узагальнені швидкості та прискорення. Нехай задані закони зміни
в часі узагальнених координат маніпулятора. Вони, зокрема, можуть бути отримані
при розв’язку оберненої задачі вздовж траєкторії центра схвата, як це описано
в попередньому пункті. При досить великому значенні L, коли зміни узагальнених
координат на інтервалі (![]() )
малі, можна обчислити похідні за часом від узагальнених координат за формулами
кінцевих різниць. Будемо вважати, що на інтервалі (
)
малі, можна обчислити похідні за часом від узагальнених координат за формулами
кінцевих різниць. Будемо вважати, що на інтервалі (![]() )
узагальнена координата змінюється рівноприскорено:
)
узагальнена координата змінюється рівноприскорено:
де
![]() – значення узагальненої координати в моменти
– значення узагальненої координати в моменти ![]() ;
;
![]() ,
,
![]() – узагальнені швидкість та прискорення в момент tl,
що відповідають узагальненій координаті qj.
– узагальнені швидкість та прискорення в момент tl,
що відповідають узагальненій координаті qj.
Розв’язуючи систему (14.20) відносно ![]() і
і ![]() , одержуємо формули
для узагальнених швидкостей та прискорень:
, одержуємо формули
для узагальнених швидкостей та прискорень:
При інтервалах однакової тривалості, тобто коли
формули (14.21) та (14.22) спрощуються:
Приклад визначення значень узагальнених швидкостей та прискорень маніпулятора розглянутий у [17].
Швидкості та прискорення точок ланок. Визначення швидкості та прискорення точок ланок МС може здійснюватися двома наступними способами:
– через Т-матричні перетворення;
– аналітично.
Визначення швидкостей та прискорень
через Т-матричні перетворення відбувається у такій послідовності. Знаючи
узагальнені швидкості та прискорення маніпулятора, можна обчислити швидкість
та прискорення будь-якої точки будь-якої ланки i маніпулятора. Якщо
позначити через ![]() вектори
швидкості та прискорення точки ланки i в системі координат ланки 0,
то диференціюючи стовпець R0, одержуємо
(у блоковому вигляді):
вектори
швидкості та прискорення точки ланки i в системі координат ланки 0,
то диференціюючи стовпець R0, одержуємо
(у блоковому вигляді):
Диференціюючи за часом (14.7) і з погляду на те, що Ri визначає положення цікавлячої нас точки ланки i в системі координат, жорстко зв’язаній з ланкою i, і від часу не залежить, одержимо:
Механізм пошуку ![]() і
і ![]() розглянутий у [17].
розглянутий у [17].
Розв’язок прямої задачі кінематики з визначенням швидкостей та прискорень ланок наведений за допомогою алгоритму 7, показаного на рис. 14.7.
Визначення швидкостей та прискорень через аналітичні перетворення має на меті встановлення аналітичних залежностей між узагальненими координатами МС та координатами подання просторового розташування визначеної ланки (або робочого органу) МС. При цьому зазначимо, що задача розрахунку лінійних швидкостей та прискорень окремих точок МС, а також кутових швидкостей та прискорень його ланок тісно пов’язана із прямою та оберненою задачами про положення маніпулятора і також може мати пряме і обернене формулювання. При цьому в залежності від системи координат, в якій працює МС, можуть враховуватися як основні (переносні), так і допоміжні (орієнтуючі) ступені рухомості. Природно, що зі збільшенням кількості ступенів рухомості зростає і складність задач кінематики, особливо обернених.
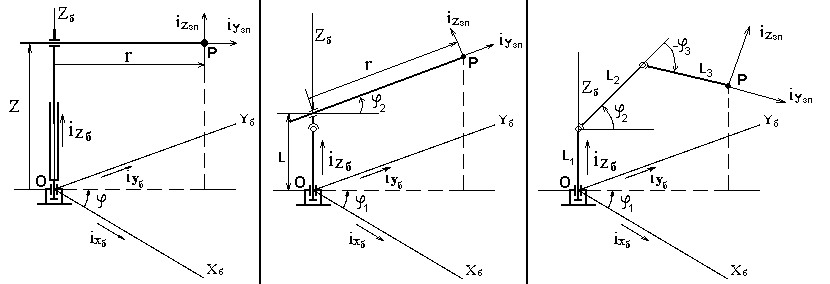
Для зручності подання та скорочення обсягу викладення зосередимося на розгляді кінематики МС із врахуванням тільки переносних ступенів рухомості. З цією метою розглянемо типові компонування триступеневих роботів, що працюють в циліндричній, сферичній та шарнірній (полярній кутовій) системах координат (рис. 14.8, а, рис. 14.8, б та рис. 14.8, в). Їх розрахункові кінематичні моделі наведені на відповідних схемах на рис. 14.9. Так, для МС з циліндричною системою координат (рис. 14.9, а) деяка точка Р (наприклад, полюс рухомої системи координат захватного пристрою) маніпулятора визначається координатами:
де r, ![]() та z
– значення узагальнених координат q1,
q17, q3
МС відповідно.
та z
– значення узагальнених координат q1,
q17, q3
МС відповідно.
Для моделі МС у сферичних координатах (рис. 14.9, б) матимемо:
де
r, ![]() ,
, ![]() – значення узагальнених координат q1, q17, q3 МС відповідно; l – відстань по осі z фіксованого розташування першої та другої пари кінематичних з’єднань
МС (або довжина відповідної ланки МС).
– значення узагальнених координат q1, q17, q3 МС відповідно; l – відстань по осі z фіксованого розташування першої та другої пари кінематичних з’єднань
МС (або довжина відповідної ланки МС).
Аналогічно для третьго компонування МС (рис. 14.9, в) координати рухомої точки Р маніпулятора будуть рівними:
|
|
(14.30)
|
де
![]() ,
,
![]() ,
, ![]() – значення узагальнених координат q1, q17,
q3 МС відповідно; l1, l17, l3 – довжини ланок МС.
– значення узагальнених координат q1, q17,
q3 МС відповідно; l1, l17, l3 – довжини ланок МС.
На підставі співвідношень (14.28)–(14.30) розв’язують пряму і обернену задачі.
Диференціюючи послідовно співвідношення (14.28)–(14.30) за часом, можна отримати вектори швидкості VЗП та прискорення WЗП точки Р:
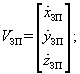 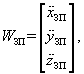
|
(14.31) |
задані своїми проекціями на осі опорної системи координат, що визначається ортами ix, iy, iz (див. рис. 14.9).
На практиці іноді (у випадку необхідності, наприклад, розрахунку зусиль ЗП для утримання об’єкта без перенавантаження в області полюса рухомих координат ЗП) важливим є задання швидкості та прискорення точки Р проекціями на осі власної рухомої системи координат, прив’язаної до ЗП. Тоді:
– для циліндричної системи координат (рис. 14.9, а):
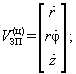 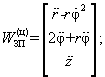
|
(14.32) |
– для сферичної системи координат (рис. 14.9, б):
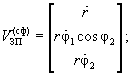 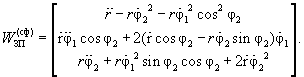
|
(14.33) |
Приклад 14.1. Розглянемо обернену задачу кінематики для МС, модель якої наведена на рис. 14.9, а.
Нехай у відповідності до технологічного процесу необхідно забезпечити
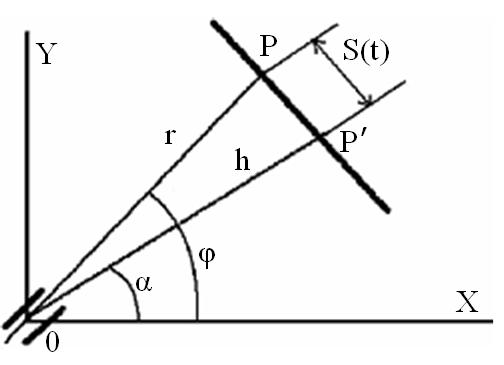
в робочій зоні рух ЗП МС по прямолінійній траєкторії. Враховуючи незалежність
руху по координаті z (узагальнена координата q3), розглянемо рух ЗП у горизонтальній площині, паралельній 0xy
(на рис. 14.10 траєкторія точки Р показана жирною
лінією). Тоді h та ![]() – параметри
траєкторії, відповідно найкоротша відстань (перпендикуляр) від початку координат
до траєкторії, а також кут нахилу напряму перпендикуляра до осі 0x;
S(t) – координата, яка відлічується по траєкторії
від точки
– параметри
траєкторії, відповідно найкоротша відстань (перпендикуляр) від початку координат
до траєкторії, а також кут нахилу напряму перпендикуляра до осі 0x;
S(t) – координата, яка відлічується по траєкторії
від точки ![]() перетину перпендикуляра та траєкторії. Узагальнені координати МС q1 = r;
q17 =
перетину перпендикуляра та траєкторії. Узагальнені координати МС q1 = r;
q17 = ![]() пов’язані з параметрами траєкторії та законом руху за нею співвідношеннями:
пов’язані з параметрами траєкторії та законом руху за нею співвідношеннями:
| |
(14.34) |
Послідовно диференціюючи співвідношення (14.34), отримаємо вирази для визначення швидкостей та прискорень по ступенях рухомості МС:
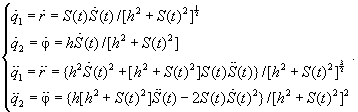 |
(14.35) |
Вирази (14.34) та (14.35)
визначають програмні закони зміни узагальнених координат, швидкостей та прискорень
МС. Очевидно, що параметри траекторії h, 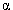 та закон S(t)
руху ЗП по ній мають бути такими, щоб виконувалися конструктивні обмеження:
та закон S(t)
руху ЗП по ній мають бути такими, щоб виконувалися конструктивні обмеження:
| |
(14.36) |
і обмеження, обумовлені можливостями приводів:
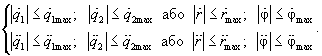 |
(14.37) |
Нехай рух ЗП здійснюється з постійною швидкістю V, тобто:
| |
(14.38) |
Підставляючи (14.38) у вирази (14.36), можна отримати граничні значення для модулів швидкостей та прискорень по ступенях рухомості МС:
| |
(14.39) |
| |
(14.40) |
які мають задовольняти умови (14.37). Крім того, можна з (14.34) та (14.35) отримати кінематичні співвідношення:
| |
(14.41) |
які
завжди виконуються незалежно від значень параметрів траєкторії h,
![]() та швидкості
V руху ЗП по ній.
та швидкості
V руху ЗП по ній.
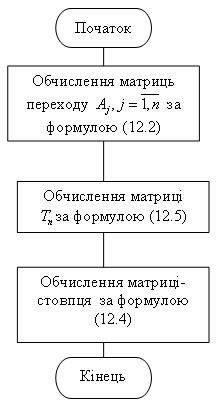
Рис. 14.2. Алгоритм розв’язування прямої задачі кінематики (визначення положення та орієнтації схвату в системі відліку, пов’язаній зі стійкою): алгоритм 2
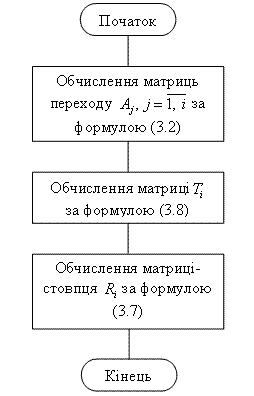
Рис. 14.3. Алгоритм розв’язування прямої задачі кінематики (визначення положення та орієнтації довільної ланки в системі відліку, пов’язаній зі стійкою): алгоритм 3
Рис. 14.4. Алгоритм розв’язування прямої задачі кінематики (визначення положення та орієнтації ланки l відносно ланки i): алгоритм 4
Рис. 14.5. Алгоритм розв’язування оберненої задачі кінематики: алгоритм 5
Рис. 14.6. Алгоритм визначення законів зміни узагальнених координат при русі по заданій траєкторії: алгоритм 6
Рис. 14.7. Схема алгоритму розв’язання прямої задачі кінематики
при визначенні швидкостей та прискорень ланок: алгоритм 7 Рис. 14.8.
Типові компонування триступеневих роботів, що працюють в циліндричній (а),
сферичній (б) та шарнірній (полярній кутовій) (в) системах координат Рис.
14.9. Розрахункові кінематичні моделі для циліндричної (а), сферичної (б)
та шарнірної (полярної кутової) (в) систем координат Рис. 14.10. Рух ЗП у горизонтальній площині 0xy