4.2. Класифікація основного ТО і вимоги до нього

    Для встановлення відповідності між груповими операціями і основним ТО необхідно створити базу даних по ТО. Для цього необхідно класифікувати вимоги до ТО і сформувати їх у групи: для геометричних і робочих характеристик — у вигляді нерівностей, для організаційних — у вигляді ознак, наявність яких необхідна для виконання операції.

    Процедури класифікації найбільш трудомісткі, тому необхідно застосовувати автоматизовані методи, які розроблені на даний момент, а також накопичений досвід створення баз даних ТО.

    4.2.1. Розподіл операцій по ГВМ

    Розподіл операцій по ГВМ здійснюється за допомогою наступної процедури. Поставимо у відповідність кожній послідовності операцій послідовність символів, що відповідають технологічним операціям у термінах конкретних типів основного ТО. Наприклад:

    Т1 Ф2 С4 - токарна, фрезерна і свердлильна операції (індекси вказують взаємозамінне ТО).

    В результаті формується список, який описує послідовність групових операцій для всіх деталей, випуск яких повинна забезпечити ГВС. Потім цей список аналізується з метою виділення елементів, що повторюються, у вигляді ланцюжків: “у всіх списках”; “в обмеженій кількості списків”.

    Набори елементів першого типу доцільно реалізувати у вигляді ГВМ на базі обробного центра або визначеної кількості основного ТО. Набори другого типу реалізуються аналогічно за умови достатнього коефіцієнта використання основного ТО. У протилежному випадку кожен елемент ланцюжка реалізується за допомогою окремого ГВМ.

    Розглянемо приклад. Нехай списки, що відповідають технологічним процесам виготовлення трьох деталей групи, мають вигляд:

Деталь 1 – Т2 С1 Ф3 Т3 С3 Ф1 Т4 Ф2 С4
Деталь 2 – Т2 С1 Ф3 С3 Ф1 С4 Ф4 Т5
Деталь 3 – Т2 С1 Ф3 Т3 С3 Ф1 С4 Ф4 Т5

    Очевидно, що повторювані у всіх списках фрагменти доцільно реалізувати на окремих ГВМ:

ГВМ-1 – <Т2 С1 Ф3>;

ГВМ-2 – <Т3 С3 Ф1> або ГВМ-2’ – <Т3>; ГВМ-2’’ – <C3 Ф1>;

ГВМ-3 – <С4 Ф4 Т5> або ГВМ-3’ – <С4>; ГВМ-3’’ – <Ф4 Т5>;

ГВМ-4 – <Т4>;

ГВМ-5 – <Ф2>.

    Таким чином, доцільно мати п’ять ГВМ, причому у випадку недовантаження ГВМ-2 і ГВМ-3 вони можуть бути розбиті на ГВМ-2', ГВМ-2" і ГВМ-3', ГВМ-3" чи використані як резерв.

    4.2.2. Вибір варіантів складу основного ТО

    Вибір складу основного ТО є однією з найважливіших задач проектування ГВС, рішення якої визначає її структурно-компонувальна побудова, вид транспортно-складської системи, системи керування ГВС тощо.

    Багатоваріантність цієї задачі обумовлює рішення її, на даному етапі, не як оптимізаційної, а як вибору ефективних варіантів складу основного ТЗ із врахуванням того, що остаточний вибір може бути здійснений лише на підставі проектування ГВМ.

    Задача вибору ефективних варіантів складу основного ТЗ із врахуванням того, що остаточний вибір може бути здійснений лише на підставі проектування ГВМ.

    Задача вибору ефективних варіантів складу основного ТЗ ГВС відповідно до його модульної структури розпадається на декілька задач, кожна з яких зводиться до призначення ТЗ до ГВМ. Розглянемо задачу вибору ефективних варіантів складу основного ТЗ ГВМ. Рішення цієї задачі розкладається на два етапи:

    1 етап – визначення необхідних фондів робочого часу по операціях;
    2 етап – вибір основного ТЗ.

    На першому етапі список, що описує послідовності групових операцій, перетвориться в список послідовності обробки деталей у ГВМ. Потім для кожного ГВМ визначається сукупність послідовностей групових операцій з його використанням. І нарешті, для кожного ГВМ заповнюється таблиця “Операція – необхідний фонд робочого часу”. Наприклад, для ГВМ-1, що реалізує набір <Т2 С1 Ф3>: <Т2 С1 Ф3>

    Вид ТЗ

    Необхідний фонд робочого часу      Т2           С1           Ф3
                                                                  Т_{порт т2}    Т _{порт с1}   Т_{порт ф3}

Де Т_{порт м} = N_i · t_imz_u
N_i - кількість деталей, що мають і-у операцію та випускаються ГВС протягом року;
t_im - максимальний час, необхідний для виконання і-ої операції виду m (m = Т2, C1, Ф3, ...).

    На другому етапі зважується задача про призначення, що у теоретико-множинній інтерпретації має наступний вигляд.
    Є множина операцій ПРО = ПРО₁, ПРО₂, ПРО₃, ПРO_n, реалізованих даними ГВМ, і деяка множина ПР = ПР₁, ПР₂, ..., ПР_m, елементу ПР_j якого відповідає одиниця основного ТО, що дозволяє реалізувати деякий кінцевий набір операцій на множині ПРО: ПР = O_j1, O_j2, ..., O_jk, які мають вартість С_j.

    Потрібно знайти покриття множини ПРО множинами ПР ПРО, тобто визначити набір: Рк = П_i1, П_i2, ..., П_k такий, що 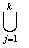ПР_ij = ПРО, а сума C_ij – мінімальна.