2.2.2.1. Формулювання задачі календарного планування
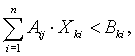 j = 1,m, k = 1,T. j = 1,m, k = 1,T. |
(2.13) |
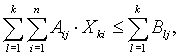 j = 1,m, k = 1,T, j = 1,m, k = 1,T, |
(2.14) |
тобто обсяг j-го ресурсу, використаного за k інтервалів, не повинен перевищувати обсягу, який надійшов до k-го інтервалу.
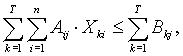 j = 1,m
j = 1,m
або
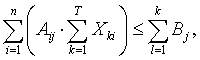 j = 1,m, j = 1,m, |
(2.15) |
де
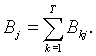
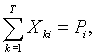 i = 1,n. i = 1,n. |
(2.16) |
| Xki ≥ 0, k = 1,T, i = 1,n. | (2.17) |
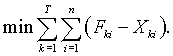 |
(2.18) |
2.2.2.2. Метод задачі календарного планування
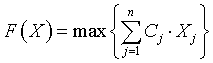 |
(2.19) |
за умов:
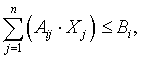 i = 1,m; i = 1,m; |
(2.20) |
| Xj ≥ 0, j = 1,n; | (2.21) |
| Xj – цілі числа. | (2.22) |