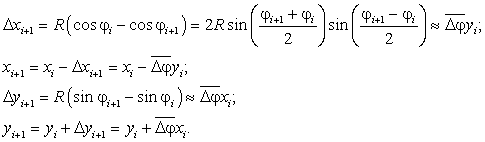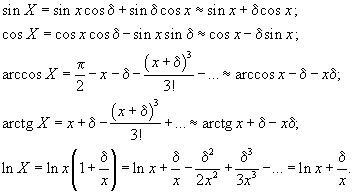Кругова інтерполяція методом оцінної функції. При круговій інтерполяції рівняння відтвореної траєкторії буде мати вигляд:
0 = (yi2 – y02) + (xi2 – x02),
а оцінна функція:
Fi = (yi2 – y02) + (xi2 – x02),
де xi, yi – координати поточної точки кола;
x0, y0 – координати початкової точки дуги відносно її центра.
У випадку руху в I квадранті проти годинникової стрілки отримаємо такі вирази для оцінної функції:
– при кроці по осі Х координата xi+1 = xi – 1, а оцінна функція:
Fi+1 = (yi2 – y02) + [(xi – 1)2 – x02]
= Fi – 2xi + 1.
– при кроці по осі Y координата yi+1 = yi + 1, а оцінна функція:
Fi+1 = [(yi + 1)2 – y02] + (xi2 – x02) = Fi + 2yi + 1.
Оскільки початкове значення оцінної функції дорівнює нулю, усі наступні значення цієї функції визначаються поточними координатами траєкторії інтерполяції.
Як випливає з наведених формул і алгоритму, на кожному кроці потрібно обчислити тільки одну змінну F. Усього можливо вісім варіантів обходу чотирьох квадрантів кола; правила вибору напрямку кроку для цих випадків зазначені на рис. 6.21.
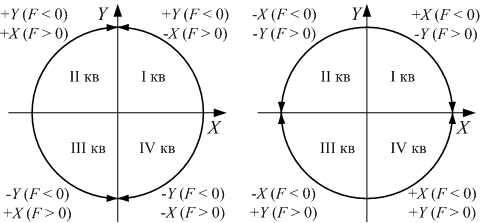
| Рис. 6.21. |
Правило вибору кроку при інтерполяції з оціночною функцією
в залежності від напрямку руху та квадранта |
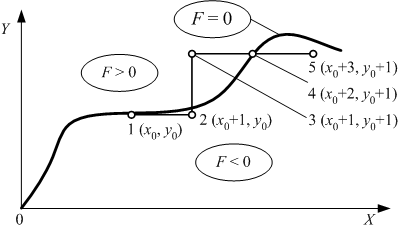
Кругова інтерполяція методом оцінної функції полягає в наступному (рис. 6.22). Коло, на якому розташований відрізок дуги, що інтерполюється, розділяється площиною XY на дві області: F > 0, що лежить поза колом, і область F < 0, що лежить в середині кола; саме коло є областю, де F = 0. Відрізок дуги, що інтерполюється, має початкову точку з координатами x0, y0 і кінцеву точку з координатами xk, yk (початок відносних координат знаходиться в центрі кола).
Якщо проміжна точка траєкторії інтерполяції (наприклад, точка з координатами (x1, y3)) знаходиться в області F > 0, то наступний крок робиться по осі X. Якщо ж проміжна точка траєкторії інтерполяції (наприклад, точка з координатами (x2, y3)) знаходиться в області F < 0, то наступний крок робиться по осі Y.
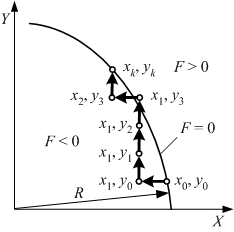
| Рис. 6.22. |
Кругова інтерполяція методом оцінної функції |
Узагальнений алгоритм інтерполяції за методом оцінної функції представлений на рис. 6.23.
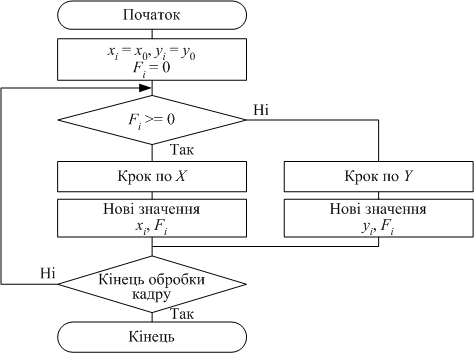
| Рис. 6.23. |
Алгоритм інтерполяції методом оцінної функції |
За кожний поточний відрізок часу лінійно-круговий інтерполятор повинен відпрацьовувати один з чотирьох можливих режимів:
| Лінійна інтерполяція |
| |
Режим 1 (F > 0) |
|
Режим 2 (F < 0) |
| 1. |
Крок по осі X |
1. |
Крок по осі Y |
| 2. |
Fi+1 = Fi – Y |
2. |
Fi+1 = Fi + X |
| 3. |
xi+1 = xi + 1 |
3. |
yi+1 = yi + 1 |
| 4. |
Перевірка xi+1 = X |
4. |
Перевірка yi+1 = Y |
| Кругова інтерполяція |
| |
Режим 3 (F > 0) |
|
Режим 4 (F < 0) |
| 1. |
Крок по осі X |
1. |
Крок по осі Y |
| 2. |
Fi+1 = Fi – 2xi + 1 |
2. |
Fi+1 = Fi + 2yi + 1 |
| 3. |
xi+1 = xi – 1 |
3. |
yi+1 = yi + 1 |
| 4. |
Перевірка xi+1 = X |
4. |
Перевірка yi+1 = Y |
Алгоритм інтерполяції методом оцінної функції досить просто реалізується програмно або апаратно. Всі операції режиму виконуються одночасно протягом одного періоду роботи. У випадку схемного виконання інтерполяції тривалість одного періоду роботи визначається часом обертання кодів у регістрах зсуву, на яких побудований інтерполятор. За цей час повинен бути встановлений потрібний режим роботи, коди чисел, що містяться в регістрі (наприклад, код величини поточної координати xi), повинні бути виведені з нього шляхом зсуву з одночасним виконанням арифметичних операцій над цими кодами (xi+1 = xi ± 1), а коди нового значення цих величин (xi+1) – введені в регістр. Введення та виведення кодів відбувається одночасно – молодший розряд нового коду йде відразу ж за старшим (знаковим) розрядом попереднього коду.
Проте, підвищені вимоги до шорсткості утворюваної поверхні вимагають заміни покоординатного руху при інтерполяції. З цієї метою був розроблений наступний варіант методу оцінної функції із застосуванням принципу управління за ведучою і веденою координатами.
6.2.2.2. Метод оцінної функції з прогнозуючим кроком
Трикоординатні лінійно-кругові інтерполятори здійснюють лінійну інтерполяцію одночасно за трьома координатами (X, Y, Z) і кругову інтерполяцію в одній із трьох площин обробки (XY, XZ чи YZ), що обираються за програмою. Напрямок чергового кроку інтерполяції в цих інтерполяторах відбувається за методом оцінної функції з прогнозуючим кроком, причому кроки здійснюються або по одній осі, або по обох одночасно (крок по діагоналі).
Лінійна інтерполяція методом оцінної функції з прогнозуючим кроком. При лінійній інтерполяції вибирається ведуча (з найбільшою величиною переміщення) координата, відносно якої ведеться інтерполяція за двома іншими координатами. При цьому крок по ведучій координаті робиться завжди, а крок по веденій (меншій) – в залежності від знака оцінної функції. Розрізняють кроки прогнозуючі і кроки на привід подачі (робочий рух).
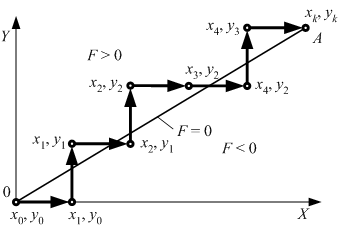
Припустимо, що в I квадранті ведучою є координата х, а веденою – у. При інтерполяції відрізка ОА прогнозуючі кроки здійснюються звичайним порядком (рис. 6.24): якщо F > 0, виконується крок по осі X; якщо F < 0, виконуються кроки по осях X, Y одночасно (тобто крок по діагоналі). Кроки на привід відстають від прогнозуючих на один такт, тобто знак оцінної функції, отриманої в результаті прогнозуючого кроку, визначає напрямок поточного кроку на привід.
Оскільки F0 = 0, перший прогнозуючий крок виконується по осі Х і перша проміжна точка траєкторії прогнозуючих кроків (x1y0) знаходиться в області F < 0. Внаслідок цього перший крок на привід виконується по діагоналі так само, як і другий прогнозуючий крок. Друга проміжна точка траєкторії (x2y1) знаходиться в області F < 0, і другий крок на привід (так само, як і третій прогнозуючий крок) виконується по діагоналі. Третій крок на привід і четвертий прогнозуючий крок виконуються по осі Х і т.д.
При прогнозуючому кроці по осі Х оцінна функція
Fi+1 = Fi – Y,
де Y – кадровий приріст координати Y, Y = yk.
При прогнозуючому кроці по осі Х і Y (по діагоналі) оцінна функція
Fi+1 = Fi – Y + X,
де X – кадровий приріст координати X, X = xk.
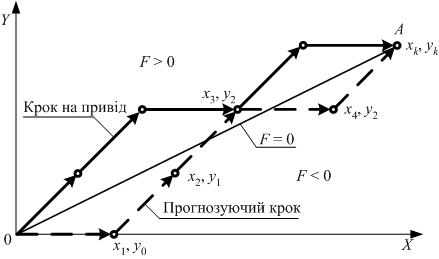
| Рис. 6.24. |
Лінійна інтерполяція методом оцінної функції з прогнозуючим кроком |
Отже, загалом алгоритм лінійної інтерполяціїї з прогнозуючим кроком наступний:
– якщо F > 0 або F = 0, то наступний прогнозуючий крок виконується по ведучій координаті;
– якщо F < 0, то наступний прогнозуючий крок виконується одночасно по ведучій та веденій координатам;
– крок на привід відстає на один такт від прогнозуючого і відповідає наступному прогнозуючому кроку.
Кругова інтерполяція методом оцінної функції з прогнозуючим кроком. Кругова інтерполяція дещо відрізняється від лінійної тим, що необхідно враховувати той факт, що при проходженні лінії переключення (зміни координатами ролей) ведуча і ведена координати міняються місцями. Тому при круговій інтерполяції застосовується два окремих алгоритми проведення розрахунку.
При круговій інтерполяції проти годинникової стрілки в першому за напрямком руху напівквадраті першого квадранта (рис. 6.25), для якого максимальним координатним переміщенням є зсув по осі Y, кроки виконуються або по осі Y, або по діагоналі. Якщо у проміжній точці траєкторії прогнозуючих кроків F > 0, то видається прогнозуючий крок по діагоналі, якщо F < 0 – по осі ведучої координати Y. Кроки на привід видаються після виділення нового значення оцінної функції і збігаються за напрямком з наступним прогнозуючим кроком.
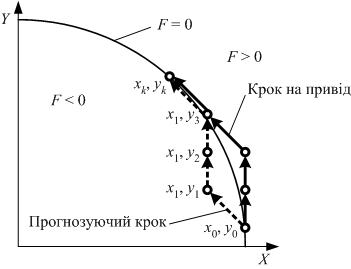
| Рис. 6.25. |
Кругова інтерполяція методом оцінної функції з прогнозуючим кроком |
При прогнозуючому кроці по осі Y координата рівна yi+1 = yi + 1, а оцінна функція:
Fi+1 = Fi + 2yi + 1.
При прогнозуючому кроці по діагоналі координати змінюються yi+1 = yi + 1, xi+1 = xi – 1, а оцінна функція рівна:
Fi+1 = Fi + 2yi – 2xi + 2.
При круговій інтерполяції проти годинникової стрілки в другому за напрямком руху напівквадраті першого квадранта кроки здійснюються: при F > 0 – по осі ведучої координати Х, а при F < 0 – по діагоналі.
При прогнозуючому кроці по осі Х координата xi+1 = xi – 1, оцінна функція:
Fi+1 = Fi – 2xi + 1.
Кроки по діагоналі в кожному окремому випадку обираються з метою кращого (плавного) наближення до заданої траєкторії, що інтерполюється. Одночасний рух по обох осях призводить до зниження похибки апроксимації кола та прямої.
Враховуючи, що кругова інтерполяція може виконуватися у двох напрямках руху за і проти годинникової стрілки, існує 8 варіантів застосування алгоритмів проведення розрахунків інтерполяції (рис. 6.26). Узагальнений алгоритм кругової інтерполяції складається з наступних режимів:
Режим 1 (точки знаходяться до лінії переключення координат):
– якщо F > 0 або F = 0, то прогнозуючий крок виконується по ведучій та веденій координатах;
– якщо F < 0, то прогнозуючий крок виконується по ведучій координаті.
Режим 2 (точки знаходяться після лінії переключення координат):
– якщо F > 0 або F = 0, то прогнозуючий крок виконується по ведучій координаті;
– якщо F < 0, то прогнозуючий крок виконується по ведучій та веденій координатах;
– крок на привід відстає на один такт від прогнозуючого і відповідає наступному прогнозуючому кроку.
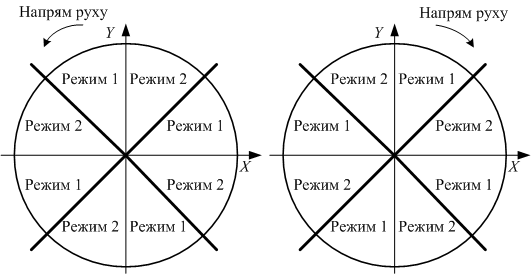
| Рис. 6.26. |
Правило застосування алгоритму кругової інтерполяції методом оцінної функції з прогнозуючим кроком |
Аналіз показує, що використання фіксованого циклу із розрахунку одного кроку інтерполяції в межах кожного циклу ставить надмірно високі вимоги щодо швидкодії обчислювача або накладає обмеження на швидкісні можливості верстата, змушуючи зменшувати частоту фіксованих циклів. Тому метод оцінної функції в чистому вигляді можна використовувати лише при апаратній реалізації інтерполятора.
6.2.2.3. Метод оцінної функції на постійній несучій частоті
Інша можливість застосування ідеї методу оцінної функції полягає у використанні модифікованого алгоритму, що працює на постійній несучій частоті. При цьому інтерполятор в кожному періоді видає у слідкуючі приводи цифрові паралельні коди.
Постійну несучу частоту вибирають з таким розрахунком, щоб виконавчі слідкуючі приводи верстата виконували роль природного фільтра, що згладжує дискретний характер управління.
Наприклад, нехай постійна несуча частота складає 100 Гц. У цьому випадку для приводів верстата як командні будуть сформовані не окремі поодинокі імпульси, а пачки імпульсів або міжтактові прирости, обсяги яких залежать від співвідношення контурної швидкості та несучої частоти, а також від заданої траєкторії. Керуючі сигнали, що містять інформацію про міжтактові прирости, будуть надходити до виконавчих приводів у паралельному коді з частотою 100 Гц. Однак, динамічні властивості виконавчих приводів такі, що дискретні керуючі сигнали на вході, квантовані за часом і рівнем, будуть згладжені і монотонно відтворені на виході.
Загальний алгоритм інтерполяції методом оцінної функції на постійній несучій частоті побудований за блоковим принципом. При цьому набір блоків, що залучаються у процесі інтерполяції, визначається орієнтацією площини інтерполяції (при лінійній одночасно за трьома координатами і при круговій в одній із трьох площин обробки) і видом інтерполяції.
Лінійна інтерполяція методом оцінної функції на постійній частоті. Розглянемо процес інтерполяції прямолінійної ділянки, заданого кадровими приростами координат Х та Y, а також часом τ відпрацьовування кадру. Цей час може бути обчислений у блоці позациклових розрахунків за заданою в кадрі швидкістю подачі. Для системи, що працює на постійній несучій частоті з періодом Т, міжтактові прирости Δxi, Δyi у деякому i-му циклі інтерполяції зв’язані наступними залежностями:
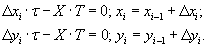
Підсумовування міжтактових приростів від початку кадра до i-го циклу інтерполяції дозволяє перейти до наступних формул:
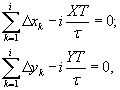
де 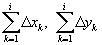 – сумарні переміщення відтворюючої траєкторію точки за координатами Х і Y від початку кадру до i-го циклу періоду постійної несучої частоти.
– сумарні переміщення відтворюючої траєкторію точки за координатами Х і Y від початку кадру до i-го циклу періоду постійної несучої частоти.
Якщо врахувати, що інтерполяція ведеться по цілих числах, то взагалі праві частини цих рівнянь не є нульовими і їх необхідно позначити відповідно через Ni та Mi. В результаті отримаємо систему оцінних функцій:
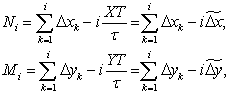
де 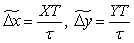 – середні міжтактові прирости відповідних координат, які повинні відпрацьовуватися у кожному циклі інтерполяції, тобто оцінна функція показує сумарне відхилення у прирості координати за певну кількість циклів (різницю між відпрацьованим і заданим).
– середні міжтактові прирости відповідних координат, які повинні відпрацьовуватися у кожному циклі інтерполяції, тобто оцінна функція показує сумарне відхилення у прирості координати за певну кількість циклів (різницю між відпрацьованим і заданим).
Беручи до уваги наведені вирази, стратегію управління для чергового i-гo циклу можна побудувати наступним чином:
– якщо Ni > 0, то 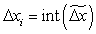 , інакше
, інакше 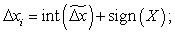
– якщо Mi > 0, то 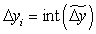 , інакше
, інакше 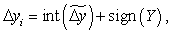
де функція int здійснює виділення цілої частини числа, а функція sign дорівнює одиниці зі знаком, що збігається зі знаком аргументу функції.
З наведених формул випливає, що чергові міжтактові прирости Δxi і Δyi є цілими числами дискрет. Отже, і середні міжтактові прирости також повинні вимірюватись у дискретах. Звичайно, кадрові прирости X, Y задаються в мм, контурна швидкість V у мм/хв, період постійної частоти T – у сек, а дискретність d – у мм, що необхідно врахувати у формулах визначення середніх міжтактових приростів:
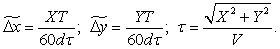
В результаті алгоритм лінійної інтерполяції буде полягати у паралельному розрахунку тактових приростів всіх координат для поточного циклу інтерполяції:
– прийняти для поточного i-го циклу попередні значення тактових приростів координат 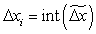 ,
, 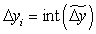 ;
;
– розрахувати значення оцінних функцій Mi та Ni;
– якщо значення оцінної функції від’ємне, то скоригувати попередне значення тактового приросту координати додавши одну дискрету, інакше остаточним значенням приросту стане попереднє значення.
Слід врахувати, що кількість циклів інтерполяції у кадрі визначається як:
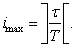
Тривалість останнього циклу може бути менша, ніж значення періоду T. Тому тактові прирости координат для останього циклу визначаються як:
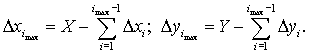
Кругова інтерполяція методом оцінної функції на постійній частоті. Розглянемо процес інтерполяції дуги кола при русі проти годинникової стрілки в першому квадранті. Для кругової інтерполяції в площині (X, Y) відносного i-го періоду справедливі наступні вирази, що випливають з чисто геометричних співвідношень:
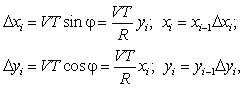
де V – контурна швидкість подачі;
xi, yi – поточні координати відтворюючої точки дуги кола в i-му циклі інтерполяції (відносно центра кола);
φ – поточний кут відтворюючої точки дуги, що відліковується проти годинникової стрілки від позитивного напрямку осі X;
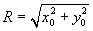 – радіус дуги кола;
– радіус дуги кола;
x0, y0 – координати початкової опорної точки дуги кола.
Представлені формули є аналітичною формою запису умови руху по запрограмованій дузі кола із заданою швидкістю контурної подачі.
Підсумовування міжтактових приростів аж до i-гo циклу призводить до наступних рівнянь:
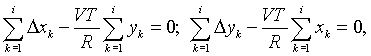
де 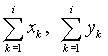 – накопичені до i-го циклу суми поточних координат відтворюючої точки дуги кола.
– накопичені до i-го циклу суми поточних координат відтворюючої точки дуги кола.
Переходячи до оцінних функцій для кожної координати, що визначають сумарне відхилення від заданої траєкторії руху, отримаємо наступну систему рівнянь:
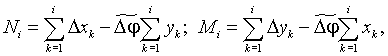
де параметр 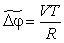 представляє собою середній та постійній в межах всього кадру приріст кута повороту відтворюючої точки за період T несучої частоти вздовж дуги запрограмованого кола.
представляє собою середній та постійній в межах всього кадру приріст кута повороту відтворюючої точки за період T несучої частоти вздовж дуги запрограмованого кола.
Наведені вирази оцінних функцій показують складність проведення кругової інтерполяції порівняно з лінійною, що визначається у взаємозалежності проведення розрахунків координат не тільки між собою, а й від поточних їх значень.
Тому вид оцінних функцій дозволяє сформулювати наступну стратегію управління для чергового i-го циклу: встановити Δxi = 0 і розрахувати значення оцінної функції (вона повинна бути від’ємна), після чого послідовно збільшуємо Δxi, доти, поки Ni > 0, що відповідає остаточному значенню Δxi, який передаємо у вихідний регістр. Процедура визначення Δyi за своїм змістом аналогічна.
Виходячи з того, що розрахунки для кожної координати є взаємозалежними, їх виконують паралельно, використовуючи результати однієї координати для іншої і навпаки.
Ступінь врахування значень інших координат дозволяє створити декілька варіантів алгоритмів з різною похибкою у розрахунках.
Один із таких варіантів алгоритмів розрахунків з найбільшим ступенем врахування значень координат може бути таким:
1) нехай для i-го циклу інтерполяції Δxi = 0 і Δyi = 0;
2) розрахувати xi = xi-1 – Δxi, yi = yi-1 + Δyi, а потім Ni, Mi;
3) якщо Ni ≥ 0 та Mi ≥ 0, то Δxi та Δyi є кінцевими значеннями координатних приростів і цикл інтерполяції завершено;
4) якщо Ni < 0, то Δxi = Δxi + 1, якщо Mi < 0 – Δyi = Δyi + 1; виконати перехід до п. 2.
Отже, схему інтерполяції методом оцінної функції на постійній несучій частоті можна подати як процес вироблення компенсацій на кожному кроці циклів інтерполяції з метою недопущення відхилень від заданої траєкторії руху (знак оцінної функції на кожному кроці повинен бути додатним). Внаслідок цього інтерполяційна траєкторія буде пролягати переважно зверху над заданою траєкторією для модифікованих методів оцінної функції. Крім того, оцінні функції Ni, Mi оцінюють накопичену похибку інтерполяції у порівняні з функцією Fi, яка оцінює похибку інтерполяції тільки поточного кроку, тобто метод оцінної функції на постійній несучій частоті повинен більш точно відтворювати задану траєкторію руху, ніж інші методи оцінної функції.
6.2.2.4. Метод цифрових диференціальних аналізаторів
При інтерполяції за методом цифрових диференціальних аналізаторів (ЦДА) моделюється диференціальне рівняння відтвореної кривої, рішення якого і є задана відтворена крива.
Метою створення цього методу є підвищення точності відпрацювання заданих складних кривих (від 2 порядку і вище). Ідея полягає у зниженні порядку кривої заданого руху і наступної інтерполяції за рахунок інтегрування різницевих рівнянь, що задані координатами кінцевих точок. Наслідком цього є включення в загальну структурну схему розрахунків координат пристрою – диференціатора (рис. 6.27). Враховуючи те, що метод ЦДА призначено для підвищення точності відтворення складних кривих, його робота реалізована на постійній несучій частоті.
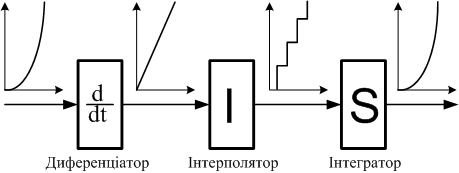
| Рис. 6.27. |
Загальна структурна схема реалізації методу ЦДА |
Загальний метод побудови диференціальних рівнянь, розв’язком яких є задані криві, описаний В.С. Кулебакіним і названий методом К (D)-перетворення. Для найпростіших же траєкторій (прямої та кола) диференціальні рівняння можуть бути знайдені прямим способом.
Лінійна інтерполяція методом ЦДА. Відтворемо схему реалізації методу ЦДА для алгебраїчного рівняння прямої лінії:
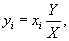
де X, Y – кадрові прирості координат.
Продиференціюємо рівняння по х і отримаємо диференціальне рівняння прямої лінії:
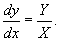
Перейдемо до параметричних диференціальних рівнянь:
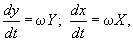
де 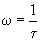 – параметр диференціальних рівнянь;
– параметр диференціальних рівнянь;
τ – повний час відпрацьовування кадру.
Приведемо систему параметричних рівнянь до вигляду:
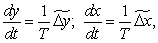
де T – період постійної частоти;
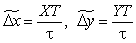 – середні міжтактові прирости по відповідних координатах, що мають цілі та дробові частини, підраховані з високою точністю.
– середні міжтактові прирости по відповідних координатах, що мають цілі та дробові частини, підраховані з високою точністю.
Проінтегруємо обидві частини рівнянь і отримаємо наступні вирази для координат точок траєкторії руху:
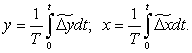
При обчисленні інтеграла скористаємося наближенням Ейлера і перейдемо до дискретного часу. Отримаємо наступні вирази для координат точок кожного циклу інтерполяції на постійній несучій частоті:
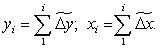
Таким чином, обчислення поточних координат xi, yi відтворюючої точки здійснюється додаванням середніх міжтактових приростів, а реалізацію методу ЦДА для лінійної інтерполяції можна провести за допомогою двох програмно чи апаратно побудованих регістрів-накопичувачів, що і є цифровим диференціальним аналізатором.
Наведені вище вирази продемонстрували методичну сутність побудови цифрового диференціального аналізатора.
В основу реального алгоритму лінійної інтерполяції за методом ЦДА покладені наступні залежності:
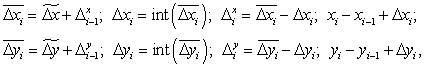
де 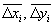 – повні величини приростів
координат, що містять дробову і цілу частини дискрет;
– повні величини приростів
координат, що містять дробову і цілу частини дискрет;
Δxi, Δyi – цілі частини приростів координат, що призначені для видачі у i-му циклі інтерполяції на постійній несучій частоті;
Δix, Δiy – накопичувачі дробових залишків координат;
іnt – операція виділення цілої частини, що полягає у відкиданні дробового залишку;
xi, yi – накопичувач координат.
Отже, алгоритм лінійної інтерполяції методом ЦДА полягає у проведенні паралельних розрахунків координат за наступними кроками:
– визначення повних приростів координат 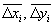 із врахуванням дробових залишків від попередній циклів інтерполяції;
із врахуванням дробових залишків від попередній циклів інтерполяції;
– визначення приростів координат Δxi, Δyi та їх дробових частин Δix, Δiy, які будуть використані в наступному інтерполяційному циклі;
– видача керуючих сигналів івизначення значень координат xi, yi.
В рамках алгоритму здійснюється перевірка кінця відпрацьовування кадру, тобто для останнього циклу інтерполяції координатні прирости розраховуються як:
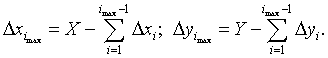
Таким чином, схему інтерполяції методом ЦДА можна подати як процесс накопичення відхилень на кожному кроці циклів інтерполяції та вироблення корегуючього впливу (компенсації), коли це накопичення досягне значення однієї дискрети. Внаслідок цього інтерполяційна траєкторія буде пролягати переважно нижче заданої траєкторії.
Кругова інтерполяція методом ЦДА. Розглянемо за такою ж схемою побудову методу ЦДА для кругової інтерполяції траєкторії руху проти годинникової стрілки у першому квадранті.
Рівняння кола з радіусом R записується наступним алгебраїчним виразом:
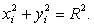
Після диференціювання по х отримаємо:
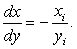
Переходимо до параметричних диференціальних рівнянь від параметра 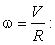
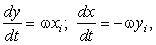
де V – контурна швидкість подачі.
Перетворимо систему параметричних рівнянь із врахуванням введення середнього приросту кута повороту відтворюючої точки за період T постійної частоти інтерполятора 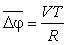 до вигляду:
до вигляду:
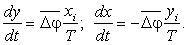
Проінтегруємо обидві частини параметричних рівнянь і отримаємо наступні вирази для координат точок траєкторії руху:
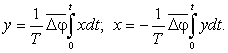
При обчисленні інтеграла скористаємося наближенням Ейлера і перейдемо до дискретного часу. Отримаємо наступні вирази для координат точок кожного циклу інтерполяції на постійній несучій частоті:
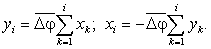
Від’ємний знак у виразі координати X показує на те, що абсолютне значення координати зменшується, а прирости координат отримують значення:
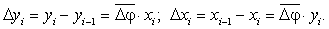
Наведені рівняння є описом цифрового диференціального аналізатора. Операція підсумовування виконується в кожному новому циклі періоду постійної несучої частоти. При цьому в регістр-накопичувач подається значення поточної координати відтворюючої точки.
Структурна схема зв’язків у цифровому диференціальному аналізаторі при круговій інтерполяції наведена на рис. 6.28. Звернемо увагу на те, що в регістрі-накопичувачі координати Y здійснюється підсумовування поточних координат xi, а в регістрі-накопичувачі координати Х – yi.
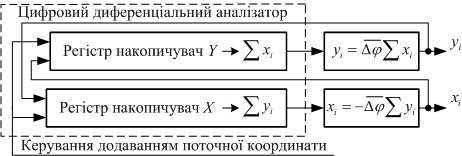
| Рис. 6.28. |
Структурна схема зв’язків у цифровому диференціальному аналізаторі при круговій інтерполяції |
Метод цифрових диференціальних аналізаторів трактують звичайно більш широко, відносячи до цього методу такі алгоритмічні структури з апаратно чи програмно реалізованими регістрами-накопичувачами, у рамках яких (мова йде про структури) відбувається підсумовування дуже точно підрахованих координат чи їх приростів, виділення для керування приводами цілих частин, накопичення дробових залишків тощо. Іншими словами, цифровий диференціальний аналізатор як пристрій, що моделює диференціальне рівняння відтвореної траєкторії, може в явному вигляді не виявлятися. Проте власне алгоритмічну структуру отримують на підставі суто геометричного підходу без залучення диференціальних форм.
Розглянемо один з варіантів кругової інтерполяції, що належить до методу ЦДА (рис. 6.29). Інтерполяція здійснюється на постійній несучій частоті з періодом T. З кожним періодом постійної несучої частоти відбувається приріст 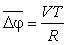 кута повороту відтворюючої точки, де використані уже введені раніше значення. Цей кут повороту може бути заданий його косинусом, а той, у свою чергу, підрахований на етапі підготовки інтерполяції за допомогою розкладу в ряд:
кута повороту відтворюючої точки, де використані уже введені раніше значення. Цей кут повороту може бути заданий його косинусом, а той, у свою чергу, підрахований на етапі підготовки інтерполяції за допомогою розкладу в ряд:
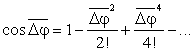
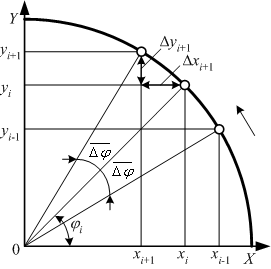
| Рис. 6.29. |
Кругова інтерполяція методом ЦДА |
Можна скористатися також табличними значеннями косинусів, збереженими в пам’яті пристрою ЧПУ.
Поставимо задачу визначення міжтактових приростів Δxi+1, Δyi+1 геометричним шляхом:
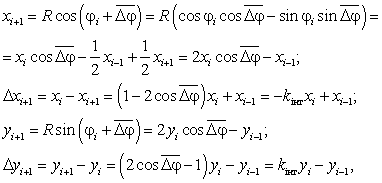
де  – коєфіцієнт кругової інтерполяції, який розраховується на початку кадру.
– коєфіцієнт кругової інтерполяції, який розраховується на початку кадру.
Наведені формули залучаються до рекурсивних процедур розрахунку чергових приростів на підставі попередніх значень поточних координат, що зберігаються і коригуються у регістрах-накопичувачах. Якщо врахувати, що кожне розраховане значення координат виконане з деякою похибкою, то з аналізу виразу для обчислення координат видно, що ця похибка входить два рази. Отже, необхідно запобігти використанню у розрахунках координат інших значень, крім попередніх.
Одним з таких варіантів модифікації методу ЦДА при круговій інтерполяції є метод прогнозу та корекції.
6.2.2.5. Метод прогнозу та корекції
Кожен цикл інтерполяції за методом прогнозу та корекції складається з двох етапів: на першому етапі виробляється груба оцінка (прогноз) координат наступної точки (вузла) інтерполяції, а на другому ці координати коригуються з метою підвищення точності та виключення можливості нагромадження похибок.
Таким чином, задача побудови алгоритму інтерполяції зводиться до вибору методу прогнозу та методу корекції координат наступного вузла. Загальна ідея алгоритму показана на рис. 6.30.
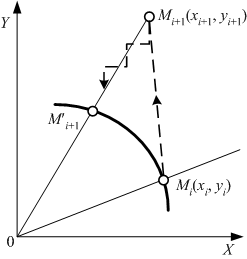
| Рис. 6.30. |
Інтерполяція за методом прогнозу та корекції |
На першому етапі за допомогою спрощеної модифікації методу ЦДА роблять прогнозуючий крок вздовж дотичної до траєкторії у поточній точці Mi:
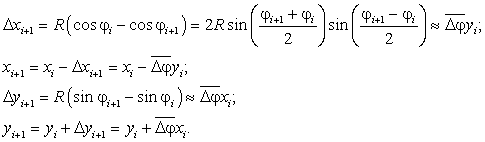
Якщо точка Mi(хi, yi) належить дузі кола радіуса R, то точка Mi+1(хi+1, yi+1) знаходиться поза колом радіуса R, оскільки перший наближений етап інтерполяції здійснюється вздовж дотичної до точки Mi.
Тому на другому етапі здійснюється лінійна інтерполяція поодинокими кроками в напрямку до центра О кола вздовж прямої Мi+11О. Інтерполяція закінчується при зміні знака оцінної функції Fк, початкове значення якої в точці Mi+1 складає Fк = xi+12 + yi+12 – R 2.
Лінійна інтерполяція уздовж прямої Мi+1О проводиться з використанням оцінної функції Fл = yi+1x – xi+1y, де x, у – координати поточної точки траєкторії лінійної інтерполяції.
У процесі лінійної інтерполяції на кожному кроці по осі Х (при Fл < 0) виконуються такі операції:
Fк = Fк – 2x + 1; Fл = Fл + yi+1; x = x – 1.
Аналогічно на кожному кроці на осі Y (при Fл > 0 або Fл = 0) виконуються такі операції:
Fк = Fк – 2y + 1; Fл = Fл – xi+1; y = y – 1.
Зміна знака функції Fк говорить про те, що точка інтерполяційної траєкторії ввійшла в коло радіуса R з відхиленням, що не перевищує однієї дискрети.
Таблично-аналітичні методи обчислення функцій. Завершуючи огляд методів інтерполяції, відзначимо, що багато з них вимагають обчислення тригонометричних і обернених тригонометричних функцій. Способи їх обчислення, що базуються на поданні функцій ступеневими рядами, ланцюговими дробами, багаточленами чи дробово-раціональними виразами, а також ітераційні способи вимагають великих витрат обчислювальної потужності. Ось чому серед них істотно виграють таблично-аналітичні методи.
Таблично-аналітичний метод обчислення функції φ передбачає:
– подання аргументу Х функції φ у вигляді двох доданків: X = x + δ, де Х – точне значення аргументу; х – найближче менше табличне значення аргументу; δ – різниця між точними і табличними значеннями аргументу;
– знаходження значення функції φ(х) за таблицею;
– обчислення значення функції φ(X) за аналітичною залежностю між φ(х) і δ.
Для визначення зазначеної аналітичної залежності функцію φ(X) представляють ступеневим рядом, який потім ділять на дві групи: перша група членів ряду відповідає φ(х), а друга представляє собою аналітичий вираз, доповнення φ(х) до φ(X). Доповнення апроксимують із врахуванням малої величини δ, необхідної точності обчислення та зручності подання в системі команд обчислювача.
Наведемо деякі функції, які зручно та доцільно реалізовувати таблично-аналітичним методом:
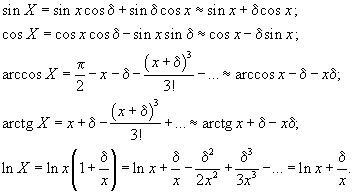
Одна з переваг таблично-аналітичного методу полягає у простоті інтерполяції складних контурів, які не вдається подати як сукупність відрізків прямих і кіл. Користуючись наведеними алгоритмами, можна формувати керуючі сигнали, що описуються квадратичними, логарифмічними, експоненціальними функціями або іншими складними законами.
Різноманітність алгоритмів інтерполяції пояснюється необхідністю компромісу між прагненням до високої точності обчислень, з одного боку, і бажанням вкластися в мінімальний за часом інтерполяційний цикл з іншого боку. Завершивши розгляд проблеми інтерполяції, перейдемо до чергової фази розв’язку геометричної задачі, що полягає в управлінні слідкуючими приводами подачі.






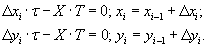
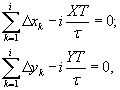
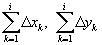 – сумарні переміщення відтворюючої траєкторію точки за координатами Х і Y від початку кадру до i-го циклу періоду постійної несучої частоти.
– сумарні переміщення відтворюючої траєкторію точки за координатами Х і Y від початку кадру до i-го циклу періоду постійної несучої частоти.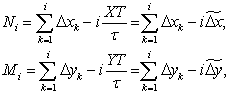
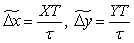 – середні міжтактові прирости відповідних координат, які повинні відпрацьовуватися у кожному циклі інтерполяції, тобто оцінна функція показує сумарне відхилення у прирості координати за певну кількість циклів (різницю між відпрацьованим і заданим).
– середні міжтактові прирости відповідних координат, які повинні відпрацьовуватися у кожному циклі інтерполяції, тобто оцінна функція показує сумарне відхилення у прирості координати за певну кількість циклів (різницю між відпрацьованим і заданим).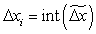 , інакше
, інакше 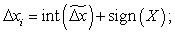
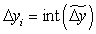 , інакше
, інакше 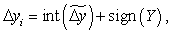
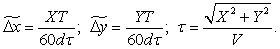
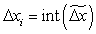 ,
, 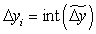 ;
;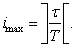
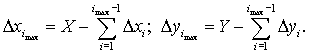
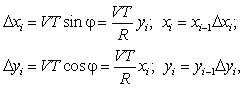
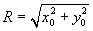 – радіус дуги кола;
– радіус дуги кола;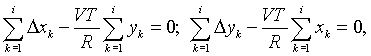
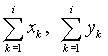 – накопичені до i-го циклу суми поточних координат відтворюючої точки дуги кола.
– накопичені до i-го циклу суми поточних координат відтворюючої точки дуги кола.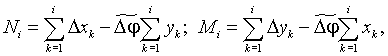
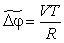 представляє собою середній та постійній в межах всього кадру приріст кута повороту відтворюючої точки за період T несучої частоти вздовж дуги запрограмованого кола.
представляє собою середній та постійній в межах всього кадру приріст кута повороту відтворюючої точки за період T несучої частоти вздовж дуги запрограмованого кола.
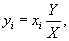
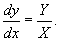
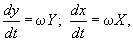
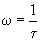 – параметр диференціальних рівнянь;
– параметр диференціальних рівнянь;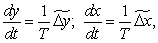
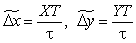 – середні міжтактові прирости по відповідних координатах, що мають цілі та дробові частини, підраховані з високою точністю.
– середні міжтактові прирости по відповідних координатах, що мають цілі та дробові частини, підраховані з високою точністю.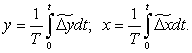
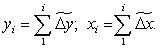
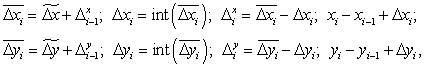
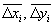 – повні величини приростів
координат, що містять дробову і цілу частини дискрет;
– повні величини приростів
координат, що містять дробову і цілу частини дискрет;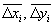 із врахуванням дробових залишків від попередній циклів інтерполяції;
із врахуванням дробових залишків від попередній циклів інтерполяції;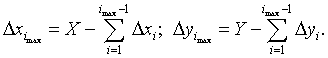
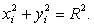
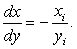
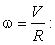
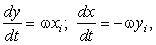
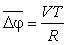 до вигляду:
до вигляду:
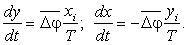
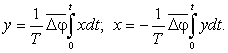
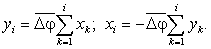
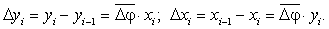

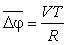 кута повороту відтворюючої точки, де використані уже введені раніше значення. Цей кут повороту може бути заданий його косинусом, а той, у свою чергу, підрахований на етапі підготовки інтерполяції за допомогою розкладу в ряд:
кута повороту відтворюючої точки, де використані уже введені раніше значення. Цей кут повороту може бути заданий його косинусом, а той, у свою чергу, підрахований на етапі підготовки інтерполяції за допомогою розкладу в ряд:
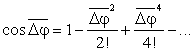

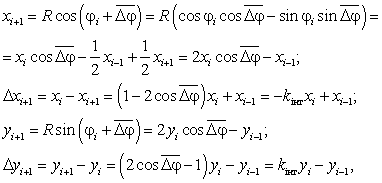
 – коєфіцієнт кругової інтерполяції, який розраховується на початку кадру.
– коєфіцієнт кругової інтерполяції, який розраховується на початку кадру.